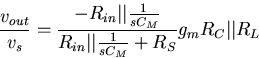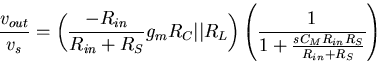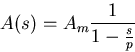Next: Miller Time Constant Approach
Up: Frequency Response of Simple
Previous: Experiment: Low Frequency Response
At high frequencies, the voltage gain of amplifiers usually
decreases. To demonstrate this consider the circuit in Fig.4.7.
Figure 4.7:
CE Amp with Miller Capacitor
 |
As we saw in the preceding sections, capacitors C1, C2 and CE
tend to give rise to increasing gain with high frequency.
Here, on the other hand,
we have another capacitor C4, which tends to cause the
gain to decrease as frequency increases. The effect of this
capacitor can be explained qualitatively by the following
discussion. Recall that the signal at the collector is
approximately 180o out of phase with the input signal
at the base. The capacitor C4 provides a path for some
of that signal at the collector to be fed back to the
base. Since collector signal is out of phase with the base
signal, this feedback has the effect of partially
canceling the input signal at the base. Since the total
signal going into the base is thus reduced, the overall
gain decreases. It can be shown that the effect of
the capacitor C4 can be approximated by the
circuit in Fig. 4.8, which is known as Miller's Approximation.
Figure 4.8:
CF Amp using Miller's Approximation
 |
The circuit shows that the effect of
C4 can be modeled by replacing it by
CM to ground, where CM is given by
Where Am is the midband gain of the amplifier stage.
For example, if the circuit in Fig. 4.7 has a midband
gain of -gmRC||RL, then CM=(gmRC||RL+1)C4.
As implied by Fig. 4.8,
the base signal then sees a low pass filter consisting
of RS, CM and Rin, thereby attenuating
the high frequency response of the circuits.
For example, the gain of the amplifier in Fig. 4.7,
assuming that the frequency is high enough so that C1, C2,
CE can be considered short circuits,
is given by
| 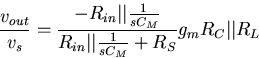 |
(82) |
It is interesting to note that Equation (4.17) can be arranged
into the following:
| 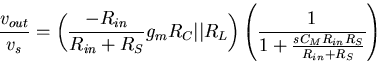 |
(83) |
By recalling the results from Chp. 2,
we can see that the expression in the first set of
parentheses is the midband
gain Am.
Furthermore, the expression in the second parentheses
is just that of a first order low pass filter, with the pole
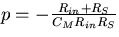 .Thus, we can express the gain of the circuit at high frequencies as
a midband gain Am multiplied by a low pass filter response.
.Thus, we can express the gain of the circuit at high frequencies as
a midband gain Am multiplied by a low pass filter response.
| 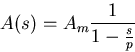 |
(84) |
The Bode plot for the high frequency response given by equation (4.18)
can quickly be drawn starting with a horizontal line of
magnitude 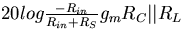 ,and then having the gain fall off with a slope of 20dB/dec at frequencies
,and then having the gain fall off with a slope of 20dB/dec at frequencies
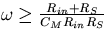




Next: Miller Time Constant Approach
Up: Frequency Response of Simple
Previous: Experiment: Low Frequency Response
Neil Goldsman
10/23/1998