University of Michigan

 Graphic: Phiroze Parakh
Graphic: Phiroze Parakh

Contemporary algorithmic composition ranges from traditional stochastic methods seen in M and Jam Factory (Zicarelli, D.) to complex rule-based systems such as EMI (Cope, D. 1987, 1992) and Cypher (Rowe, R.). This paper describes a composition process that combines the best of these two extremes, achieving the simplicity of a stochastic process and the determinism of a rule-based system.
A popular way to solve a problem, answer a question, or in general derive a suitable structure to fit a set of requirements, is to cast the problem or question as a search problem, a technique central to artificial intelligence. The goal is to look through the entire set of possible solutions to find one that satisfies the original criteria; the trick is to structure the set of all possible solutions so that one does not have to check every solution, allowing the search to complete in a finite amount of time.
One can think of the composition of music as just such a problem: consider the set of all possible compositions as the solution space, with the problem at hand being, "find a composition that sounds good." This solution space is unstructured in that good solutions may lie next to perfectly awful ones; if you change a few key notes in a piece it may become far less interesting, though on the surface it appears virtually identical. An unstructured solution space makes searching through it unpredictable and therefore difficult.
Enter the genetic algorithm (Holland, J.), an extremely effective technique for searching enormous, possibly unstructured solution spaces. The algorithm begins with randomly-generated solutions to a problem and uses the equivalent of biological recombination to find better solutions, ultimately ending up with an optimal set. The solutions are represented by chromosomes, strings of alleles represented by strings of numbers, and the recombination of chromosomes is simply a matter of creating new strings with alleles taken from the parent chromosomes. Since solutions are evolved by trying out answers and combining the answers that work best, the technique is particularly well-suited to solving "fuzzy" problems where the solution domain is poorly behaved, or where there is no clear way to judge the solutions objectively.
The technique has been used in music before: (Horner, A. 1991) describes the application of genetic algorithms to thematic transformation, (Biles, J.) describes a genetic-based jazz soloist, and (Horowitz, D.) describes a genetic algorithm for creating interesting rhythms. The biggest problem seems to be the size of the search space; successful GA-music studies have had restricted goals, because the problem domain gets large quickly and therefore convergence to a satisfactory solution may take extremely long. Horner deals with morphing one melody into another, Biles generates single melodies on top of given chord progressions, and Horowitz deals with rhythms that span only one measure. This experiment restricts the focus of the search differently; instead of reducing the size of the problem domain, this GA deals with larger building blocks.
IMPLEMENTATION: Variations
The project begins with an attempt to reduce the author's compositional processes to a few simple rules that can be easily transformed into a computer program. The following is a fair approximation:
These rules form the basis of the software system variations, depicted in Fig. 1. The composition of motives, evaluation of the music, and arranging of the piece are done by genetic agents--the composer, ear and arranger modules. The composer module produces music, the ear module filters out unsatisfactory material, and the arranger module imposes an order on whatever is left. The human operator judges the agents on their ability to produce pleasing music, and recombines successful agents to produce better agents.
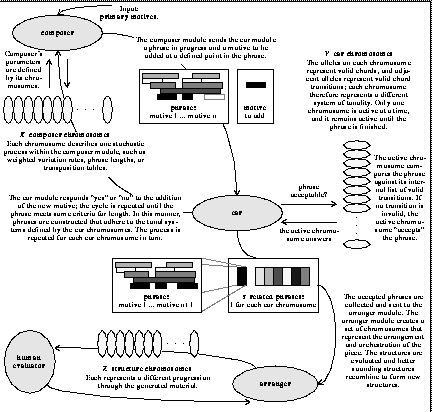
Figure 1: The algorithmic composition system variations
To make the genetic search problem feasible, one can either reduce the size of the problem domain and deal with simpler music, or one can impose a certain amount of order and work with larger building blocks. Instead of working at the note level, this experiment deals with the higher-level structures of phrases and motives. The system composes and evaluates small phrases, then arranges those phrases into larger statements. Order is imposed by ensuring that all notes in the resultant piece belong to motives related to each other through recognizable transformations such as transposition, inversion, and varied meter. This restriction guarantees that a certain amount of thematic cohesion is inherent in the resultant piece, therefore more attention and compute cycles can be placed on harmonic progression.
The composition process is straightforward. The composer and ear agents start with randomly-generated characteristics that need to be tailored to suit the tastes of the human operator. Once these are in place, composition begins. The human operator defines a set of primary motives to be used in the composition. The composer module creates variations on these motives, using them to build up phrases one motive at a time. Whenever a motive is added to a phrase, the ear module is consulted. If the ear module disapproves of the resulting harmonic content, the motive is removed. The musical output thus adheres to the systems of tonality defined by the ear's chromosomes. Once there are enough usable phrases, the arranger module creates orderings that are then evaluated and recombined to produce better orderings.
Genetic algorithms are used in each of the components, albeit in different ways. The composer module is a stochastic process that produces variations on input material. Its parameters are determined by a set of chromosomes, and its use of genetic algorithms is therefore similar to studies on parameter coupling (Horner, A. 1993). The arranger module takes as input a list of candidate phrases deemed usable and generates orderings of subsets of the list; not all phrases are used in every ordering. The "best" orderings are used to create new orderings, and so its use of genetic algorithms is similar to the use of GAs on the traveling salesman problem (Goldberg, D.; Grefenstette, J.). The ear module alone is deterministic in its behavior; it is a collection of chromosomes, each of which represents a different system of tonality. The initial chromosomes are randomly produced, and the music they create sounds accordingly random. As successive generations of ear chromosomes evolve, the ear module becomes better and better at producing coherent tonal systems.
THE EAR: A method for representing systems of tonality
The ear module is the most important piece of the system, and warrants a more detailed description.
The module is a collection of chromosomes, each of which acts as a data filter that identifies harmonic combinations as "good" or "bad." Before composition begins, the chromosomes are evolved to reflect the musical tastes of the human operator. First, a set of randomly-generated ear chromosomes are auditioned on how well they filter material. The evaluation mechanism in this process, as in virtually all other genetic music studies, is a human judge. Musical examples are created and passed through the ear chromosomes, and the human operator assigns weights to chromosomes according to how well they agree with his or her inclinations. Chromosomes with high marks are more likely to reproduce and have their alleles present in the next generation. Successive generations therefore exhibit the best traits of previous generations. Once there is a satisfactory set of filters, the process shown in Fig. 1 begins.
Chromosome structure
The alleles of the ear's chromosomes represent valid vertical pitch combinations. They are similar to interval classes, except that they include any number of pitches from one to twelve. Each allele is twelve bits long, representing a set of semitones that can be played simultaneously. Every two adjacent alleles indicate a valid unidirectional transition. Like interval classes, all twelve transpositions of a valid pitch combination (or transition between two combinations) are also valid. For example, if two adjacent alleles indicate that
is a valid transition, then the following are also considered valid:
However, the following are not:
A piece of music is accepted by an ear chromosome if the chromosome finds every transition in the piece valid. The music is first collapsed into a single octave. The ear module checks vertical pitch combinations at the resolution of an eighth note. During every eighth note every sounding verticality, whether an attack or sustaining pitch, is considered part of the combination. The vertical pitch combination is represented by an integer; each note in a twelve-tone octave corresponds to a bit in the first twelve bits of an integer. Therefore, any transition that is a subset of a valid transition is easily and quickly identified by anding the representations together. If the transition is not a subset, then each of its twelve transpositions are compared in turn.
Microtonal applications
The system is extremely flexible. Note that the general representation of valid combinations is not dependent on the choice of a twelve-tone octave. One can represent microtonal vertical pitch combinations by simply using a different number of bits in the representation. For example a 19-bit allele corresponds to an octave divided into 19 semitones. Since valid combinations of vertical pitches are chosen by identifying which ones "sound good" rather than by a rule-based method (which may or may not make sense in a microtonal scenario), the ear is a viable approach to composing microtonal pieces. One can also produce different tonal systems in different registers by changing the current implementation of collapsing all notes into a single octave before validation. This method fails to recognize that dissonant pitches are less noticeable when widely separated.
RESULTS: System output, current work
Fig. 2a gives four excerpts of compositions produced by the system. Fig. 2b shows the ear chromosome and 2c shows the primary motives used to produce the pieces. The examples give an indication of how the final motives typically resemble those from which they are derived. The transformations tend to be recognizable but certainly not obvious. Current work investigates beyond simple transformation of motives, toward the development of motives and thematic material.
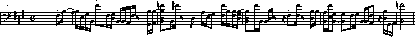
Figure 2a: Four musical examples of variations output
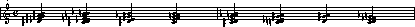
Figure 2b: Ear chromosome used to create the examples above

Figure 2c: Primary motives used to create the examples above
Acknowledgments
This project owes much of its musical vision to the guidance of Evan Chambers, and the paper would not have been readable without his editing skills.
References