 Force-Displacement Response of Material Softening Composite Bar
Force-Displacement Response of Material Softening Composite Bar
 Force-Displacement Response of Material Softening Composite Bar
Force-Displacement Response of Material Softening Composite Bar
[ Problem Statement ]
[ Solution Procedure ]
[ Matrix Force-Displacement Calculation ]
[ Finite Element Calculation ]
[ Input/Output Files ]
You will need Aladdin 2.0 to run this problem.
In this example we will compute the force-displacement relationship for a material softening bar that must transfer an axial force P to its wall support.
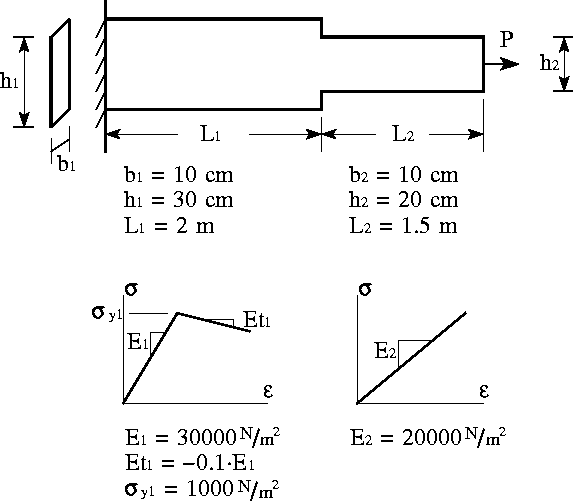
Figure 1 shows the bar geometry, and a summary of the section and material properties.
The cross section areas are 300 cm^2 and 200 cm^2 for elements 1 and 2, respectively. The composite bar is constructed from two materials. Incipient yielding of the left-most material occurs at 1000 N/m^2. The right-most material remains linear elastic.
Force-Displacement Calculation
Rather than simply compute the nonlinear bar displacements caused by an applied force "P", in this example we will apply a series of incremental displacements and for each step compute the distribution of internal forces required for equilibrium.
The latter process is known as element state determination and in this example it will be computed in two ways:
Steps 1 and 2 should generate identical numerical solutions of course.
It is important to bear in mind that while this problem looks trivial, standard stiffness-based elements have difficulty computing a displacement that satisfies equilibrium of the section forces because assumed distributions of force-displacement deviate significantly from actual displacements, especially in the post-yielding region.
These difficulties can be circumvented with a flexibility-based formulation customized for implemention in a standard finite-element program. The key steps are:
[ K ] . d_p = d_E.
The update in global displacements is:
p = p + d_p;
d_q = [ L ] . d_p
where the matrix [ L ] relates structural displacements to element deformations.
d_Q = [ K ] . d_q
Here [ K ] is the stiffness matrix at the end of the previous loop of state determination.
Q = Q + d_Q
dD(x) = b(x).Q(x)
D(x) = D(x) + dD(x)
dd(x) = r(x) + f(x)*D(x)
The update in section deformations is:
d(x) = d(x) + dd(x)
f(x) = [ k(x) ]^{-1}
D_u(x) = D(x) - D_r(x)
r(x) = f(x).D_u(x)
from the section flexibility and the section unbalanced force.
End : Loop for section flexibility and unbalanced forces
If some sections have not converged, the residual element deformations "s" are determined by integration of the residual section deformations r(x) along the element length. That is:
s = integral from 0 to L { b^t (x). r(x) } dx
then set
d_q = -s
Return to top of element state determination loop.
End : Loop for state determination of all elements.
[ P_r ] = sum over structure elements { [ L_e ]^T.[ Q_e ] }.
[ K ] = sum over structure elements { [ L_e ]^T.[ k_e ].[ L_e ] }.
Here [ L_e ] is the transformation of the element displacements in the global reference system "p" to element deformations "q".
End : Loop for incremental displacements.
A detailed description of the step-by-step solution procedure can be found in Filippou et al. [1], and in Chapter 4 of Wane-Jane Lin's Ph.D. dissertation [2].
Material/Section Properties and Initial Stiffness
The element material and section properties are simply defined by the block of code:
/* Plastic spring material, Bi-linear */ L1 = 2 m; h1 = 30 cm; b1 = 10 cm; A1 = b1*h1; E1 = 30000 N/m^2; Et1 = -0.1*E1; fy1 = 1000 N/m^2; Ks1 = E1*A1/L1; Kt1 = Et1*A1/L1; Fy1 = fy1*A1; es1 = Fy1/Ks1; /* Elastic spring material */ L2 = 1.5 m; h2 = 20 cm; b2 = 10 cm; A2 = h2*b2; E2 = 20000 N/m^2; Et2 = E2; fy2 = 2500 N/m^2; Ks2 = E2*b2*h2/L2;
With the element level stiffnesses in place, the initial global stiffness matrix is given by:
/* Assemble initial structure tangent stiffness matrix BigK */
BigK = [ Ks1+Ks2, -Ks2;
-Ks2, Ks2 ];
and is:
MATRIX : "BigK"
row/col 1 2
units N/m N/m
1 7.16667e+02 -2.66667e+02
2 -2.66667e+02 2.66667e+02
Initial Displacement Increment
We now apply a small unit force to the right-hand side of the bar and compute the system displacement, i.e.,
d_P = [ 0 N ; 1 N]; d_p = Solve( BigK, d_P );
The output is:
MATRIX : "d_p"
row/col 1
units
1 m 2.22222e-03
2 m 5.97222e-03
Main Loop for Incremental Displacements
The following looping construct systematically increases the bar displacement, and then performs the state determination. A summary of the matrix code is:
index = 0;
for ( k = 1; k <= total_step ; k = k+1 ) {
p = p + d_p;
/* State determination for each element */
for( ele = 1 ; ele <= 2; ele = ele+1 ) {
/* extract element displacements from global displacements */
if( ele==1 ) {
d_pe = [ 0 m; d_p[1][1] ];
}
if( ele==2 ) {
d_pe = [ d_p[1][1]; d_p[2][1] ];
}
Q = Q_saved[ele][1]; /* retrieve values from (j-1) */
q = q_saved[ele][1];
Dx = bx*Q;
dx = bx*q;
K = tangent[ele][1];
kx = tangent[ele][1];
fx = 1/kx;
rx = 0 cm;
DUx = 1E+7 N;
d_q = QuanCast(L*d_pe); /* element deformation increment */
q = q + d_q;
/* convergence of forces for element "ele" */
while( abs(DUx) > 0.00001 N ) {
d_Q = K*d_q; /* element force increment */
Q = Q + d_Q; /* update element force */
/* determine the section force increments */
/* repeat for all integration points of the element */
d_Dx = bx*d_Q; /* section force increment */
d_dx = rx + fx*d_Dx; /* section deformation increment */
Dx = Dx + d_Dx; /* update section force */
dx = dx + d_dx; /* update section deformation vector */
/* get new section tangent flexibility f(x) from new d(x) */
/* and section resisting force DR(x) from material properties */
if( ele == 1 ) {
if( abs(dx) <= es1 ) {
kx = Ks1;
fx = 1/kx;
DRx = kx*dx;
}
if( dx > es1 ) {
kx = Kt1;
fx = 1/kx;
DRx = Fy1 + kx*(dx-es1);
}
if( dx < -es1 ) {
kx = Kt1;
fx = 1/kx;
DRx = -Fy - kx*(dx+es1);
}
}
if( ele == 2 ) {
kx = Ks2;
DRx = kx*dx;
}
DUx = Dx - DRx; /* section unbalanced force */
rx = fx*DUx; /* section residual deformation */
/* finish for all integration points of the element */
/* update the element flexibility and stiffness matrices */
F = bx*fx*bx;
K = 1/F;
/* check for element convergence */
s = bx*rx; /* element residual deformation */
d_q = -s;
} /* j */
Q_saved[ele][1] = Q;
q_saved[ele][1] = q;
tangent[ele][1] = K;
PRe[ele][1] = Q; /* element resisting force */
}
/* Assemble structure resistant force */
PR[1][1] = PRe[1][1] - PRe[2][1];
PR[2][1] = PRe[2][1];
/* Store output in response matrix */
response[k+1][1] = PR[2][1];
response[k+1][2] = p[2][1];
response[k+1][3] = p[1][1];
response[k+1][4] = p[2][1] - p[1][1];
/* Calculate new delta displacement after yielding */
if( index == 1 ) {
d_P[1][1] = 0 N;
d_P[2][1] = -1 N;
d_p = Solve( BigK, d_P );
index = 0;
}
/* Adjust delta displacement at yielding step */
if( abs(PR[1][1]) > 0.01 N ) {
/* assemble new structure stiffness */
BigK[1][1] = tangent[1][1] + tangent[2][1];
BigK[1][2] = -tangent[2][1];
BigK[2][1] = -tangent[2][1];
BigK[2][2] = tangent[2][1];
index = 1;
k = k-1;
d_p[1][1] = 0 cm;
d_p[2][1] = PR[1][1]/tangent[2][1];
}
}
Points to note:
Force-Displacement Relationship
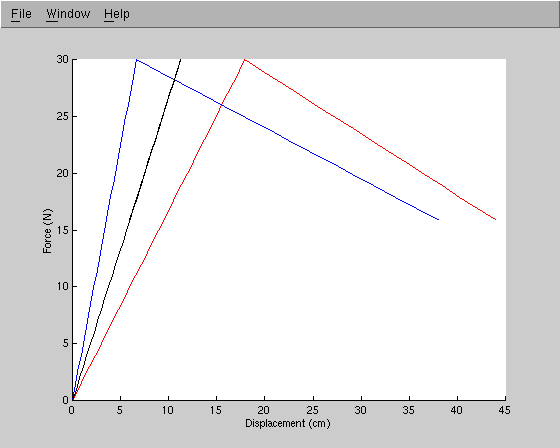
The three lines in Figure 2 show the force displacement curves for element 1 (in blue), element 2 (in black), and the total system (in red).
Points to note:
We can see that after the softening material starts to yield, the resistant force drops with further increases in the bar elongation. Also notice that at all times the blue and black displacements sum to the red displacement.
We use the variable "index" to keep track of when the system traverses a change in system stiffness. The post yielding stiffness is:
MATRIX : "BigK"
row/col 1 2
units N/m N/m
1 2.21667e+02 -2.66667e+02
2 -2.66667e+02 2.66667e+02
External Load versus Step Number
The axial load versus time step is shown in Figure 3.
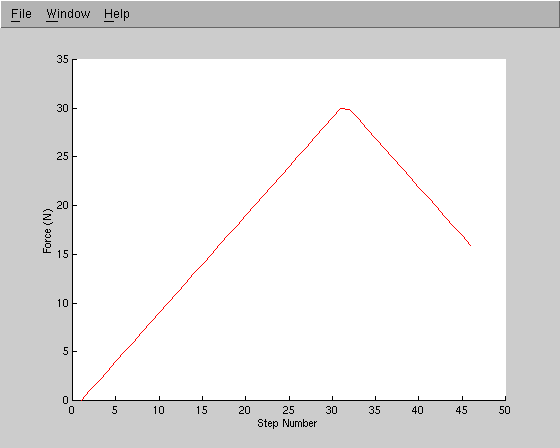
We expect that incipient yielding of the bar will occur when the axial force reaches
F = 1000 N/m^2 * 300 x 10^-4 m^2 = 30 N.
Problem Specification Parameters
The block of code:
NDimension = 2;
NDofPerNode = 3;
MaxNodesPerElement = 2;
GaussIntegPts = 2;
defines parameters for a two-dimensional problem involving finite elements having 2 nodes and three-degrees of freedom per node. The parameter GaussIntegPts defines the number of locations for which the section flexibility will be evaluated along a fiber element.
Finite Element Mesh
The abbreviated block of code:
L1 = 2 m; L2 = 1.5 m; /* Generate grid of nodes for finite element model */ AddNode(1, [ 0 m, 0 m]); AddNode(2, [ L1, 0 m]); AddNode(3, [ L1+L2, 0 m]); /* Attach elements to grid of nodes */ AddElmt( 1, [1, 2], "elmt_attr1"); AddElmt( 2, [2, 3], "elmt_attr2");
generates a finite element mesh containing three nodes and two FIBER_2D finite elements having the attribute names "elmt_attr1" and "elmt_attr2" (details given below).
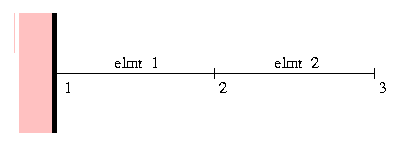
Figure 4 shows an elevation view of the finite element mesh.
Fiber Section and Material Properties
The abbreviated block of code:
ElementAttr("elmt_attr1") { type = "FIBER_2D";
section = "section1";
material = "material1";
fiber = "fib_name1"; }
SectionAttr("section1") { width = b1; depth = h1; area = b1*h1; }
MaterialAttr("material1") { poisson = 0.25;
E = E1; Et = Et1; yield = fy1; }
no_fiber = 4; no_fiber_type = 1;
b = b1; h = h1; dh = h/no_fiber;
ks = E1; kt = Et1; fy = fy1;
fcoord = Matrix([ 1, no_fiber ]);
farea = Matrix([ 1, no_fiber ]);
fmap = Matrix([ 1, no_fiber ]);
for( i=1 ; i <= no_fiber ; i=i+1 ) {
fcoord[1][i] = h/2 - dh/2 - (i-1)*dh;
farea[1][i] = b*h/no_fiber;
fmap[1][i] = 1;
}
fattr = Matrix([ 3, 1 ]);
for( j=1 ; j <= no_fiber_type ; j=j+1 ) {
fattr[1][j] = ks;
fattr[2][j] = kt;
fattr[3][j] = fy;
}
FiberAttr( no_fiber, "fib_name1" ) { FiberMaterialAttr = fattr;
FiberCoordinate = fcoord;
FiberArea = farea;
FiberMaterialMap = fmap; }
shows how the section and material propoerties are defined, and how the individual beam elements are partitioned into 4 fiber elements.
The layout of fibers within each element is shown in Figure 5.
Force-Displacement Calculation
Now that we know the algorithm works well on a computationally difficult problem, the next step is to implement the fiber element and the iterative solution procedure in ALADDIN's finite element library. The input statements for the whole solution procedure will be reduced to:
for( step=1 ; step <= total_step ; step = step + 1 ) {
/* Increment displacement by "dp" */
displ = displ + dp;
/* State determination for all elements */
ElmtStateDet( dp );
/* Assemble structure resistant force */
PR = InternalLoad( displ );
PrintMatrix(PR);
/* Update element information */
UpdateResponse();
/* Store displacements in "response" matrix */
response[step+1][1] = PR[dof2][1];
response[step+1][2] = displ[dof2][1];
response[step+1][3] = displ[dof1][1];
response[step+1][4] = displ[dof2][1] - displ[dof1][1];
/* Calculate new delta displacement after yielding */
if(index == 1 ) {
NodeLoad( total_node, [ -1 N, 0 N, 0 N*m ] );
dP = ExternalLoad();
dp = Solve( Ks, dP );
index = 0;
}
/* Adjust delta displacement at yielding step */
if( abs(PR[dof1][1]) > 0.01 N ) {
Ks = Stiff(); /* assemble new structure stiffness */
index = 1;
step = step - 1;
dp[dof1][1] = 0 m;
dp[dof2][1] = PR[dof1][1]/Ks[2][2];
}
}
Points to note are:
References
Matrix Implementation
Finite Element Implementation