Analysis of Rectangular Plate Subject to Uniaxial Loading
Analysis of Rectangular Plate Subject to Uniaxial Loading
 Analysis of Rectangular Plate Subject to Uniaxial Loading
Analysis of Rectangular Plate Subject to Uniaxial Loading
[ Problem Description ]
[ Finite Element Model ]
Figure 1 shows a rectangular plate is subjected to an uniaxial load.
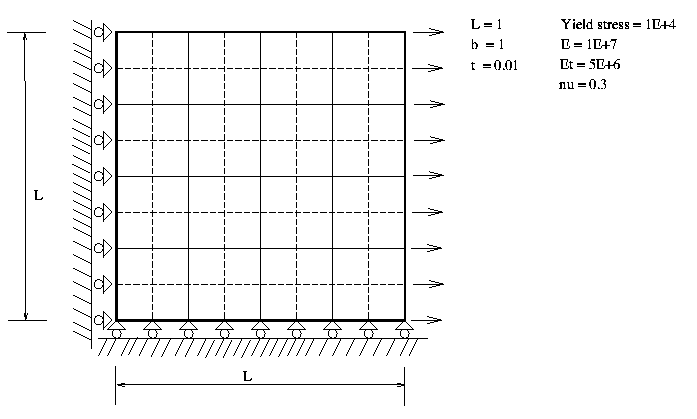
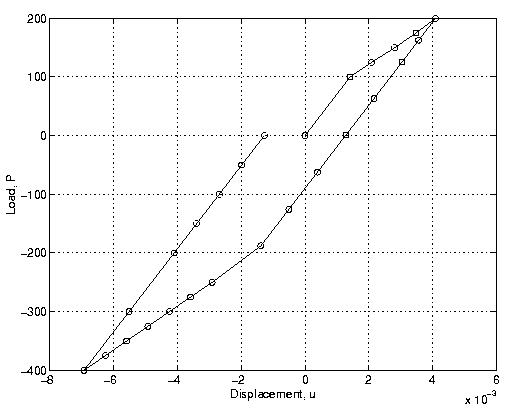
The initial load is Po = 1E+4*L*t. The total load is P = Factor*Po. The integration points in the surface are 2x2 points and in the thickness are points. Two cases are examined for the isotropic strain hardening model. The Young's modulus is E = 1E+7 and the yield stress is 1E+4 psi, Possion ratio is 0.3.
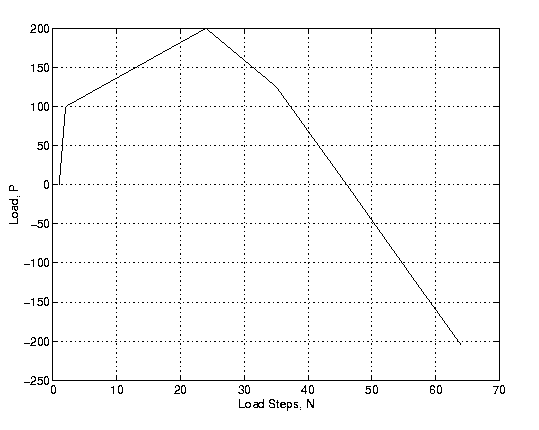
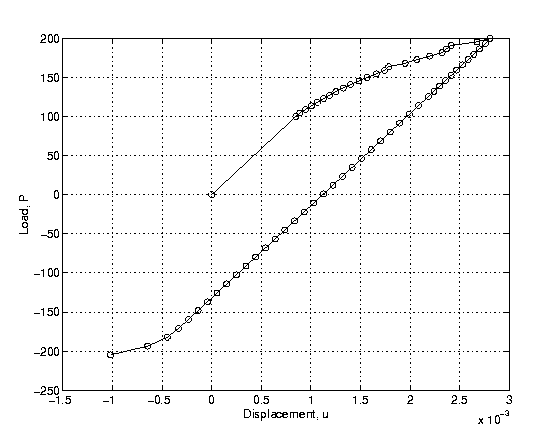
The second case is for the Ramberg-Osgood stress-strain model. The strain hardening exponent, n, and the coefficient, alpha, of the Ramberg-Osgood model are : 4 and 3/7, respectively. The load factor is given as: Factor = [1.0, 1.5, 2, 1.255, 0.01, -1.255]. Between every load factor and next load factors, the load steps are subdivided into eleven sub-steps. And the load load steps are stopped at No. 63. The load steps are shown at Figure 3, and the results is shown by Figure 4.