 Modal Analysis of a 4 Story Shear Building
Modal Analysis of a 4 Story Shear Building
 Modal Analysis of a 4 Story Shear Building
Modal Analysis of a 4 Story Shear Building
[ Problem Description ]
[ Input File ]
[ Output File ]
[ Analysis Results ]
In this example we compute the eigenvalues, natural periods of vibaration, and modal shapes for a 4 story shear building.
Figure 1 is a schematic of the 4 story shear building, and its corresponding mass and stiffness matrices.
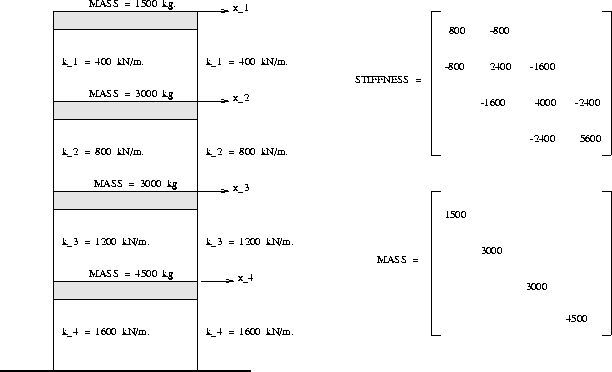
A simplified model of the building is obtained by assuming that all of the building mass is lumped at the floor levels, that the floor beams are rigid, and that the columns are axially rigid. Together these assumptions allow for the generation of a model commonly known as a shear-type building model, where displacements at each floor level may be described by one degree-of-freedom alone. Hence, only four degrees of freedom are needed to describe total displacements of the structure.
We employ a three-part input file to define the mass and stiffness matrices, solve the eigenproblem, and print the corresponding eigenvectors and natural periods of vibrations. Details of the ALADDIN input file are as follows:
/* [a] : Define working variables for eigenproblem analysis */
no_eigen = 4;
/* [b] : Form mass and stiffness matrices */
mass = ColumnUnits( 1500*[ 1, 0, 0, 0;
0, 2, 0, 0;
0, 0, 2, 0;
0, 0, 0, 3], [kg] );
stiff = ColumnUnits( 800*[ 1, -1, 0, 0;
-1, 3, -2, 0;
0, -2, 5, -3;
0, 0, -3, 7], [kN/m] );
PrintMatrix(mass, stiff);
/* [c] : Compute and print eigenvalues, natural periods of */
/* vibration, and eigenvectors. */
eigen = Eigen(stiff, mass, [no_eigen]);
eigenvalue = Eigenvalue(eigen);
eigenvector = Eigenvector(eigen);
for(i = 1; i <= no_eigen; i = i + 1) {
print "Mode", i ," : w^2 = ", eigenvalue[i][1];
print " : T = ", 2*PI/sqrt(eigenvalue[i][1]) ,"\n";
}
PrintMatrix(eigenvector);
Points to note:
We have used the parameter no_eigen to control the number of eigenvalues/vectors that are computed by the subspace iteration, and printed.
MATRIX : "mass"
row/col 1 2 3 4
units kg kg kg kg
1 1.50000e+03 0.00000e+00 0.00000e+00 0.00000e+00
2 0.00000e+00 3.00000e+03 0.00000e+00 0.00000e+00
3 0.00000e+00 0.00000e+00 3.00000e+03 0.00000e+00
4 0.00000e+00 0.00000e+00 0.00000e+00 4.50000e+03
MATRIX : "stiff"
row/col 1 2 3 4
units N/m N/m N/m N/m
1 8.00000e+05 -8.00000e+05 0.00000e+00 0.00000e+00
2 -8.00000e+05 2.40000e+06 -1.60000e+06 0.00000e+00
3 0.00000e+00 -1.60000e+06 4.00000e+06 -2.40000e+06
4 0.00000e+00 0.00000e+00 -2.40000e+06 5.60000e+06
*** SUBSPACE ITERATION CONVERGED IN 2 ITERATIONS
Mode 1 : w^2 = 117.8 1/sec^2 : T = 0.5789 sec
Mode 2 : w^2 = 586.5 1/sec^2 : T = 0.2595 sec
Mode 3 : w^2 = 1125 1/sec^2 : T = 0.1873 sec
Mode 4 : w^2 = 2082 1/sec^2 : T = 0.1377 sec
MATRIX : "eigenvector"
row/col 1 2 3 4
units
1 1.00000e+00 1.00000e+00 -9.01452e-01 1.54356e-01
2 7.79103e-01 -9.96248e-02 1.00000e+00 -4.48172e-01
3 4.96553e-01 -5.39887e-01 -1.58595e-01 1.00000e+00
4 2.35062e-01 -4.37613e-01 -7.07973e-01 -6.36879e-01
Figure 2 shows the four modal shapes of vibration and associated natural periods of vibration.
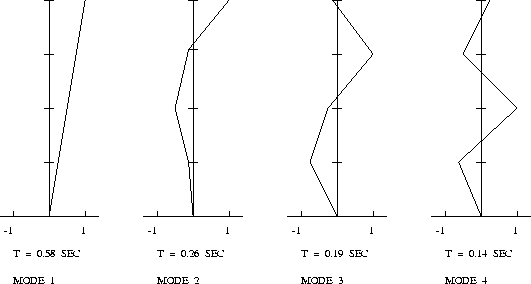
Points to note: