 Finite Element Mesh Generation
Finite Element Mesh Generation
 Finite Element Mesh Generation
Finite Element Mesh Generation
[ Getting Started ]
[ Nodes and Elements ]
[ Section and Material Properties ]
[ Boundary Conditions ]
[ External Loads ]
ALADDIN's specification parameters are:
| NDimension | Stands for the number of dimensions. For two- and three-dimensional finite element analyses, "NDimension" equals 2 and 3, respectively. |
| NDofPerNode | Stands for the maximum number of degrees of freedom per nodal coordinate. When "NDimension" equals 2, NDofPerNode will take the value 3. And when "NDimension" equals 3, "NDofPerNode" will equal 6. |
| MaxNodesPerElement | Corresponds to the maximum number of nodes per finite element. |
| InPlaneIntegPts | Corresponds to the number of in-plane integration points for shell finite elements. |
| ThicknessIntegPts | Number of layers of integration points through thickness direction of shell finite elements. |
These parameter settings are used in the allocation of memory for the finite element mesh.
Example
This example initializes the problem specification parameters for a three-dimensional analysis of a structure with an eight-node shell finite element.
/* [a] : Define Problem Specific Parameters NDimension = 3; NDofPerNode = 5; MaxNodesPerElement = 8; /* .... etc ..... */
The procedure of creating a finite element mesh is:
Two functions, AddNode() and AddElement(), are employed for the generation of finite element nodal coordinates, and the attachment of finite elements to the nodes.
AddNode( nodeno, [ coord_vector ] )
Here "nodeno" is the node number in the finite element mesh.
For two-dimensional finite element problems, coord_vector is a 1x2 matrix containing the [x, y] nodal coordinates. When the finite element problem is three-dimensional, coord_vector is a 1x3 matrix containing the [x, y, z] nodal coordinates.
AddElmt( elmtno , [ connect_vector ] , "name_of_elmt_attr" )
Here "elmtno" is the element number in the finite element mesh.
connect_vector is a 1xn matrix containing a list of "n" nodes to which the finite element will be attached. "name_of_elmt_attr" is the attribute name representing the finite element's material and section properties -- details given below.
Example
Figure 1 shows a two-dimensional coordinate system, and a line of six finite element nodes connected by 2-node beam finite elements. The nodes are located at y-coordinate = 1 m, and are spaced along the x-axis at 1 m centers, beginning at x = 1 m and finishing at x = 6 m.
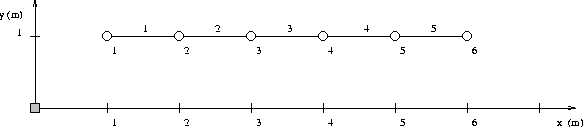
Aladdin's looping constructs are ideally suited for specification of the finite element nodes in a compact manner, and for the attachment of the two-node finite elements. Here's the code:
/* Generate grid of nodes for finite element model */
nodeno = 0;
x = 1 m; y = 1 m;
while(x <= 6 m) {
nodeno = nodeno + 1;
AddNode(nodeno, [x, y]);
x = x + 1 m;
}
/* Attach finite elements to nodes */
elmtno = 0; nodeno = 0;
while(elmtno < 5) {
elmtno = elmtno + 1; nodeno = nodeno + 1;
AddElmt( elmtno, [nodeno, nodeno + 1], "name_of_elmt_attr");
}
In the first half of the script, 6 nodal coordinates are added to ALADDIN's database. The second block of code employs the notation:
[ nodeno, nodeno + 1 ]
to generate 1 x 2 matrices containing the node numbers to which "elmtno" will be attached.
Example
Now let's suppose that we want to generate a finite element mesh for one-quarter of a circular pipe cross section. The inside and outside pipe diameters are 10 cm and 14 cm, respectively.
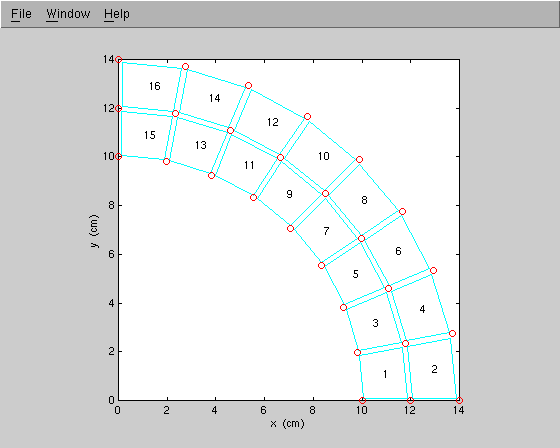
Figure 2 is a MATLAB plot of the finite element mesh we will now generate.
The block of commands:
print "*** GENERATE GRID OF NODES FOR FE MODEL \n\n";
radius_min = 10 cm; angle_min = 0.0;
radius_max = 14 cm; angle_max = PI/2;
radius_incr = 2 cm; angle_incr = PI/16;
node = 0;
angle = angle_min;
while( angle <= angle_max ) {
radius = radius_min;
while( radius <= radius_max ) {
node = node + 1;
AddNode( node, [ radius*cos(angle), radius*sin(angle) ] );
radius = radius + radius_incr;
}
angle = angle + angle_incr;
}
uses a polar coordinate system to generate 27 finite element nodes:
======================================
x-coordinate y-coordinate
Node (cm) (cm)
======================================
1 10.0 0.0
2 12.0 0.0
3 14.0 0.0
.......
25 0.0 10.0
26 0.0 12.0
27 0.0 14.0
======================================
The minimum, maximum, and incremental values of radius are represented by the variables radius_min, radius_max, radius_incr. A similar set of variables is used for the angles.
The expression:
[ radius*cos(angle), radius*sin(angle) ]
converts the polar coordinates to (x,y) cartesian coordinates.
Now that the mesh of nodes is in place, we can attach 16 finite elements to the nodes with:
nodeno = 0; elmtno = 0;
for ( i = 0; i < 8; i = i + 1 ) {
nodeno = 3*i;
for ( j = 1; j <= 2; j = j + 1 ) {
elmtno = elmtno + 1;
nodeno = nodeno + 1;
AddElmt( elmtno, [ nodeno, nodeno + 1, nodeno + 4, nodeno + 3 ], "cylinder" );
}
}
The notational scheme
[ nodeno, nodeno + 1, nodeno + 4, nodeno + 3 ]
specifies the nodal connectivity within an element anticlockwise. Hence, we have:
=============================
elmt nodal connectivity
=============================
1 1 2 5 4
2 2 3 6 5
.......
15 22 23 26 25
16 23 24 27 26
=============================
The attributes of element, section, and material types are specified with three functions, ElementAttr(), SectionAttr() and MaterialAttr(), followed by parameters inserted between braces { ... }.
The details of each function are:
ElementAttr( "name_of_element_attr" ) { ... };
Here "name_of_elmt_attr" is a character string for the name of the element attribute used in function calls to AddElmt( ... ).
Three character string arguments should be specified between the braces. "type" is a name for the finite element type (e.g., FRAME_2D for two dimensional frame elements). Character strings for the "section" and "material" attributes may taken from the section file section.h and the material file material.h, or may be user-defined with SectionAttr("...") and MaterialAttr("...").
SectionAttr( "name_of_section_attr")} { ... };
Here "name_of_section_attr" is a character string for the name of the section attribute.
===============================================================
Name Description
===============================================================
area Area of cross section.
depth Depth of section.
thickness Thickness of section.
Ixx Moment of inertia about x-x axis.
Iyy Moment of inertia about y-y axis.
Izz Moment of inertia about z-z axis.
Ixy and Iyx Moment of inertia about x-y axes.
Ixz and Izx Moment of inertia about x-z axes.
Iyz and Izy Moment of inertia about y-z axes.
rT Radius of Gyration.
tw Width of web.
tf Width of flange.
J Torsional Constant.
width Width of section.
===============================================================
Table 1 contains a list of section property names, their meaning, and the units associated with each property
MaterialAttr( "name_of_material_attr" ) { ... };
Here "name_of_material_attr" is a character string for the name of the material attribute.
===============================================================
Name Description
===============================================================
E Young's modulus of elasticity.
Et Tangent modulus of elasticity.
poisson Poisson's ratio.
density Material density.
yield Yield Stress F_y.
ultimate Ultimate Stress F_u.
n Strain Hardening Exponent
alpha Parameter for Ramberg-Osgood relationship.
beta Parameter for strain hardening
beta = 0 for kinematic hardening.
beta = 1 for isotropic hardening.
ialph Rotation constant
ialph = 0 implies none.
ialph = 1 implies Hughes rotation constant.
pen Penalty constant.
===============================================================
Table 2 contains a list of material property names, their meaning, and the units associated with each property.
Example
The script of code:
ElementAttr("floorelmts") { type = "FRAME_2D";
section = "floorsection";
material = "floormaterial";
}
SectionAttr("floorsection") { Ixy = 1 m^4;
Iyy = 2 m^4;
Ixx = 3 m^4;
Izz = 0.66666667 m^4;
depth = 2 m;
width = 1.5 m;
}
MaterialAttr("floormaterial") { E = 1E+7 kN/m^2;
density = 0.1024E-5 kg/m^3;
poisson = 1.0/3.0;
yield = 36000 psi;
}
loads a finite element attribute called "floorelmts" into ALADDIN's database. The "floorelmts" attribute has three components; the finite element type is set to FRAME_2D, for two-dimensional beam column finite elements. The element's section and material properties are defined via links to the section attribute "floorsection", and the material attribute "floormaterial".
Boundary conditions are controled through the "FixNode()" function. For each degree of freedom (DOF), an index (1 or 0) is used to indicate the fixed DOF or free DOF. The syntax for "FixNode()" is:
FixNode( nodeno , bc_vector )
Here "nodeno" is the node number to which the boundary condition will be applied. For two-dimensional problems "bc_vector" takes the form:
bc_vector = [ dx, dy, rz ]
dx and dy are the boundary condition setting in the x- and y- translational d.o.f., respectively. rz is the boundary condition setting for rotations about the z-axis. An element value of "0" means that the boundary condition is unrestrained. An element value of "1" means that the boundary condition is fully-fixed.
For three-dimensional problems "bc_vector" takes the form:
bc_vector = [ dx, dy, dz, rx, ry, rz ]
Example
The block of code:
dx = 0; dy = 1; rz = 1;
for ( ii = 1; ii <= 3; ii = ii + 1 ) {
FixNode ( ii, [ dx, dy, rz ] );
}
uses the variables dx, dy, and rz for fixity of the nodes in the horizontal, vertical and rotational degrees of freedom. dx = 0 means that the horizontal degree of freedom is unrestrained. Coversely, dy = 1 means that the vertical degree of freedom is fully fixed.
The for loop applies full fixity to nodes 1 through 3 in the vertical and rotational degrees of freedom, while leaving the horizontal degrees of freedom free to move.
External loads are applied to the nodal degrees of freedom with:
NodeLoad( nodeno , load_vector )
Here "nodeno" is the node number to which the external load will be applied. For two-dimensional problems, "load_vector" takes the form:
load_vector = [ F_x, F_y, M_z ]
F_x and F_y are forces in the x- and y- directions, respectively. M_z is a moment about the z-axis. For three-dimensional problems takes the form
load_vector = [ F_x, F_y, F_z, M_z, M_y, M_x ]
Example
The following script adds two translational forces, and one moment to nodes 1 through 5 in a two-dimensional finite element mesh.
FxMax = 1000.0 lbf;
Fy = -1000.0 lbf;
Mz = 0.0 lb*in;
for( ii = 1; ii <= 5; ii = ii + 1 ) {
Fx = (ii/5)*FxMax;
NodeLoad( ii, [ Fx, Fy, Mz ]);
}
Developed in July 1996 by Mark Austin
Copyright © 1996-2000, Department of Civil Engineering, University of Maryland